Set Interfaces

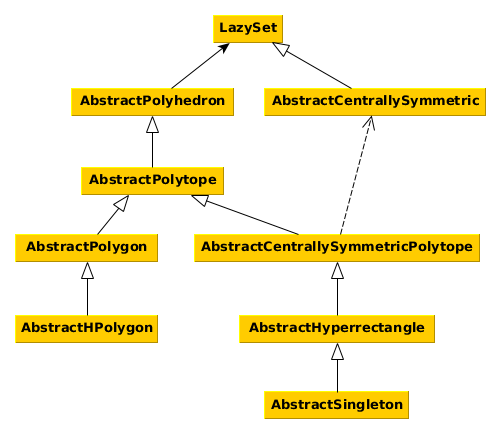
LazySet{N}

Abstract type for convex sets, i.e., sets characterized by a (possibly infinite) intersection of halfspaces, or equivalently, sets $S$ such that for any two elements $x, y ∈ S$ and $0 ≤ λ ≤ 1$ it holds that $λ·x + (1-λ)·y ∈ S$.

Notes

LazySet types should be parameterized with a type N, typically N<:Real, for using different numeric types.

Every concrete LazySet must define the following functions:

• σ(d::AbstractVector{N}, S::LazySet{N}) where {N<:Real} – the support vector of S in a given direction d; note that the numeric type N of d and S must be identical; for some set types N may be more restrictive than Real
• dim(S::LazySet)::Int – the ambient dimension of S

The subtypes of LazySet (including abstract interfaces):

julia> using LazySets: subtypes

julia> subtypes(LazySet, false)
17-element Array{Any,1}:
 AbstractCentrallySymmetric
 AbstractPolyhedron
 CacheMinkowskiSum
 CartesianProduct
 CartesianProductArray
 ConvexHull
 ConvexHullArray
 EmptySet
 ExponentialMap
 ExponentialProjectionMap
 Intersection
 IntersectionArray
 LinearMap
 MinkowskiSum
 MinkowskiSumArray
 ResetMap
 Translation

If we only consider concrete subtypes, then:

jldoctest julia> LazySets.subtypes(LazySet, true) 37-element Array{Type,1}: Ball1 Ball2 BallInf Ballp CacheMinkowskiSum CartesianProduct CartesianProductArray ConvexHull ConvexHullArray Ellipsoid EmptySet ExponentialMap ExponentialProjectionMap HPolygon HPolygonOpt HPolyhedron HPolytope HalfSpace Hyperplane Hyperrectangle Intersection IntersectionArray Interval Line LineSegment LinearMap MinkowskiSum MinkowskiSumArray ResetMap Singleton SymmetricIntervalHull Translation Universe VPolygon VPolytope ZeroSet Zonotope

support_vector

Alias for the support vector σ.

ρ(d::AbstractVector{N}, S::LazySet{N})::N where {N<:Real}

Evaluate the support function of a set in a given direction.

Input

• d – direction
• S – convex set

Output

The support function of the set S for the direction d.

Notes

The numeric type of the direction and the set must be identical.

support_function

Alias for the support function ρ.

σ

Function to compute the support vector σ.

norm(S::LazySet, [p]::Real=Inf)

Return the norm of a convex set. It is the norm of the enclosing ball (of the given $p$-norm) of minimal volume that is centered in the origin.

Input

• S – convex set
• p – (optional, default: Inf) norm

Output

A real number representing the norm.

radius(S::LazySet, [p]::Real=Inf)

Return the radius of a convex set. It is the radius of the enclosing ball (of the given $p$-norm) of minimal volume with the same center.

Input

• S – convex set
• p – (optional, default: Inf) norm

Output

A real number representing the radius.

diameter(S::LazySet, [p]::Real=Inf)

Return the diameter of a convex set. It is the maximum distance between any two elements of the set, or, equivalently, the diameter of the enclosing ball (of the given $p$-norm) of minimal volume with the same center.

Input

• S – convex set
• p – (optional, default: Inf) norm

Output

A real number representing the diameter.

isbounded(S::LazySet)::Bool

Determine whether a set is bounded.

Input

• S – set

Output

true iff the set is bounded.

Algorithm

We check boundedness via isbounded_unit_dimensions.

isbounded_unit_dimensions(S::LazySet{N})::Bool where {N<:Real}

Determine whether a set is bounded in each unit dimension.

Input

• S – set

Output

true iff the set is bounded in each unit dimension.

Algorithm

This function performs $2n$ support function checks, where $n$ is the ambient dimension of S.

an_element(S::LazySet{N}) where {N<:Real}

Return some element of a convex set.

Input

• S – convex set

Output

An element of a convex set.

plot_lazyset(S::LazySet; ...)

Plot a convex set in two dimensions using an axis-aligned approximation.

Input

• S – convex set

Examples

julia> using Plots, LazySets

julia> B = BallInf(ones(2), 0.1);

julia> plot(2.0 * B);

Algorithm

For any 2D lazy set we compute its box overapproximation, followed by the list of vertices. A post-processing convex_hull is applied to the vertices list; this ensures that the shaded area inside the convex hull of the vertices is covered correctly.

Notes

This recipe detects if the axis-aligned approximation is such that the first two vertices returned by vertices_list are the same. In that case, a scatter plot is used (instead of a shape plot). This use case arises, for example, when plotting singletons.

plot_lazyset(Xk::Vector{S}) where {S<:LazySet}

Plot an array of convex sets in two dimensions using an axis-aligned approximation.

Input

• Xk – array of convex sets

Examples

julia> using Plots, LazySets;

julia> B1 = BallInf(zeros(2), 0.4);

julia> B2 = BallInf(ones(2), 0.4);

julia> plot([B1, B2]);

Algorithm

For each 2D lazy set in the array we compute its box overapproximation, followed by the list of vertices. A post-processing convex_hull is applied to the vertices list; this ensures that the shaded area inside the convex hull of the vertices is covered correctly.

plot_lazyset(S::LazySet, ε::Float64; ...)

Plot a lazy set in two dimensions using iterative refinement.

Input

• S – convex set
• ε – approximation error bound

Examples

julia> using Plots, LazySets;

julia> B = BallInf(ones(2), 0.1);

julia> plot(randn(2, 2) * B, 1e-3);

plot_lazyset(Xk::Vector{S}, ε::Float64; ...) where {S<:LazySet}

Plot an array of lazy sets in two dimensions using iterative refinement.

Input

• Xk – array of convex sets
• ε – approximation error bound

Examples

julia> using Plots, LazySets;

julia> B1 = BallInf(zeros(2), 0.4);

julia> B2 = Ball2(ones(2), 0.4);

julia> plot([B1, B2], 1e-4);

tosimplehrep(S::LazySet)

Return the simple H-representation $Ax ≤ b$ of a set from its list of linear constraints.

Input

• S – set

Output

The tuple (A, b) where A is the matrix of normal directions and b is the vector of offsets.

Notes

This function only works for sets that can be represented exactly by a finite list of linear constraints. This fallback implementation relies on constraints_list(S).

isuniversal(X::LazySet{N}, [witness]::Bool=false
           )::Union{Bool, Tuple{Bool, Vector{N}}} where {N<:Real}

Check whether a given convex set is universal, and otherwise optionally compute a witness.

Input

• X – convex set
• witness – (optional, default: false) compute a witness if activated

Output

• If witness option is deactivated: true iff $X$ is universal
• If witness option is activated:
  • (true, []) iff $X$ is universal
  • (false, v) iff $X$ is not universal and $v ∉ X$

Notes

This is a naive fallback implementation.

==(X::LazySet, Y::LazySet)

Return whether two LazySets of the same type are exactly equal by recursively comparing their fields until a mismatch is found.

Input

• X – any LazySet
• Y – another LazySet of the same type as X

Output

• true iff X is equal to Y.

Notes

The check is purely syntactic and the sets need to have the same base type. I.e. X::VPolytope == Y::HPolytope returns false even if X and Y represent the same polytope. However X::HPolytope{Int64} == Y::HPolytope{Float64} is a valid comparison.

Examples

julia> HalfSpace([1], 1) == HalfSpace([1], 1)
true

julia> HalfSpace([1], 1) == HalfSpace([1.0], 1.0)
true

julia> Ball1([0.], 1.) == Ball2([0.], 1.)
false

copy(S::LazySet)

Return a deep copy of the given set by copying its values recursively.

Input

• S – any LazySet

Output

A copy of S.

Notes

This function performs a deepcopy of each field in S, resulting in a completely independent object. See the documentation of ?deepcopy for further details.

CompactSet

An alias for compact set types.

Notes

Most lazy operations are not captured by this alias because whether their result is compact or not depends on the argument(s).

NonCompactSet

An alias for non-compact set types.

Notes

Most lazy operations are not captured by this alias because whether their result is non-compact or not depends on the argument(s).

AbstractCentrallySymmetric{N<:Real} <: LazySet{N}

Abstract type for centrally symmetric sets.

Notes

Every concrete AbstractCentrallySymmetric must define the following functions:

• center(::AbstractCentrallySymmetric{N})::Vector{N} – return the center point

julia> subtypes(AbstractCentrallySymmetric)
3-element Array{Any,1}:
 Ball2
 Ballp
 Ellipsoid

dim(S::AbstractCentrallySymmetric)::Int

Return the ambient dimension of a centrally symmetric set.

Input

• S – set

Output

The ambient dimension of the set.

isbounded(S::AbstractCentrallySymmetric)::Bool

Determine whether a centrally symmetric set is bounded.

Input

• S – centrally symmetric set

Output

true (since a set with a unique center must be bounded).

an_element(S::AbstractCentrallySymmetric{N})::Vector{N} where {N<:Real}

Return some element of a centrally symmetric set.

Input

• S – centrally symmetric set

Output

The center of the centrally symmetric set.

isempty(S::AbstractCentrallySymmetric)::Bool

Return if a centrally symmetric set is empty or not.

Input

• S – centrally symmetric set

Output

false.

AbstractPolyhedron{N<:Real} <: LazySet{N}

Abstract type for polyhedral sets, i.e., sets with finitely many flat facets, or equivalently, sets defined as an intersection of a finite number of half-spaces.

Notes

Every concrete AbstractPolyhedron must define the following functions:

• constraints_list(::AbstractPolyhedron{N})::Vector{LinearConstraint{N}} – return a list of all facet constraints

julia> subtypes(AbstractPolyhedron)
6-element Array{Any,1}:
 AbstractPolytope
 HPolyhedron
 HalfSpace
 Hyperplane
 Line
 Universe

∈(x::AbstractVector{N}, P::AbstractPolyhedron{N})::Bool where {N<:Real}

Check whether a given point is contained in a polyhedron.

Input

• x – point/vector
• P – polyhedron

Output

true iff $x ∈ P$.

Algorithm

This implementation checks if the point lies inside each defining half-space.

constrained_dimensions(P::AbstractPolyhedron)::Vector{Int} where {N<:Real}

Return the indices in which a polyhedron is constrained.

Input

• P – polyhedron

Output

A vector of ascending indices i such that the polyhedron is constrained in dimension i.

Examples

A 2D polyhedron with constraint $x1 ≥ 0$ is constrained in dimension 1 only.

linear_map(M::AbstractMatrix{N},
           P::AbstractPolyhedron{N};
           check_invertibility::Bool=true,
           cond_tol::Number=DEFAULT_COND_TOL,
           use_inv::Bool=!issparse(M)
           ) where {N<:Real}

Concrete linear map of a polyhedron in constraint representation.

Input

• M – matrix
• P – abstract polyhedron
• check_invertibility – (optional, deault: true) check if the linear map is invertible, in which case this function uses the matrix inverse; if the invertibility check fails, or if this flag is set to false, use the vertex representation to compute the linear map (see below for details)
• cond_tol – (optional) tolerance of matrix condition (used to check whether the matrix is invertible)
• use_inv – (optional, default: false if M is sparse and true otherwise) whether to compute the full left division through inv(M), or to use the left division for each vector; see below

Output

The type of the result is "as close as possible" to the the type of P. Let (m, n) be the size of M, where m ≠ n is allowed for rectangular maps.

To fix the type of the output to something different than the default value, consider post-processing the result of this function with a call to a suitable convert method.

In particular, the output depends on the type of P, on m, and the algorithm that was used:

• If the vertex-based approach was used:

  • If P is a VPolygon and m = 2 then the output is a VPolygon.
  • If P is a VPolytope then the output is a VPolytope.
  • Otherwise, the output is an Interval if m = 1, a VPolygon if m = 2 and a VPolytope in other cases.

• If the invertibility criterion was used:

  • The types of HalfSpace, Hyperplane, Line and AbstractHPolygon are preserved.
  • If P is an AbstractPolytope, then the output is an Interval if m = 1, an HPolygon if m = 2 and an HPolytope in other cases.
  • Otherwise, the output is an HPolyhedron.

Algorithm

This function implements two algorithms for the linear map:

• If the matrix $M$ is invertible (which we check with a sufficient condition), then $y = M x$ implies $x = \text{inv}(M) y$ and we transform the constraint system $A x ≤ b$ to $A \text{inv}(M) y ≤ b$.
• Otherwise, we transform the polyhedron to vertex representation and apply the map to each vertex, returning a polyhedron in vertex representation.

Note that the vertex representation (second approach) is only available if the polyhedron is bounded. Hence we check boundedness first.

To switch off the check for invertibility, set the option check_invertibility=false. If M is not invertible and the polyhedron is unbounded, this function returns an exception.

The option use_inv lets the user control - in case M is invertible - if the full matrix inverse is computed, or only the left division on the normal vectors. Note that this helps as a workaround when M is a sparse matrix, since the inv function is not available for sparse matrices. In this case, either use the option use_inv=false or convert the type of M as in linear_map(Matrix(M), P).

Internally, this function operates at the level of the AbstractPolyhedron interface, but the actual algorithm uses dispatch on the concrete type of P, depending on the algorithm that is used:

• _linear_map_vrep(M, P) if the vertex approach is used
• _linear_map_hrep(M, P, use_inv) if the invertibility criterion is used

New subtypes of the interface should write their own _linear_map_vrep (resp. _linear_map_hrep) for special handling of the linear map; otherwise the fallback implementation for AbstractPolyhedron is used (see below).

AbstractPolytope{N<:Real} <: AbstractPolyhedron{N}

Abstract type for polytopic sets, i.e., bounded sets with finitely many flat facets, or equivalently, bounded sets defined as an intersection of a finite number of half-spaces, or equivalently, bounded sets with finitely many vertices.

Notes

Every concrete AbstractPolytope must define the following functions:

• vertices_list(::AbstractPolytope{N})::Vector{Vector{N}} – return a list of all vertices

julia> subtypes(AbstractPolytope)
4-element Array{Any,1}:
 AbstractCentrallySymmetricPolytope
 AbstractPolygon
 HPolytope
 VPolytope

isbounded(P::AbstractPolytope)::Bool

Determine whether a polytopic set is bounded.

Input

• P – polytopic set

Output

true (since a polytope must be bounded).

singleton_list(P::AbstractPolytope{N})::Vector{Singleton{N}} where {N<:Real}

Return the vertices of a polytopic set as a list of singletons.

Input

• P – polytopic set

Output

List containing a singleton for each vertex.

isempty(P::AbstractPolytope)::Bool

Determine whether a polytope is empty.

Input

• P – abstract polytope

Output

true if the given polytope contains no vertices, and false otherwise.

Algorithm

This algorithm checks whether the vertices_list of the given polytope is empty or not.

plot_polygon(P::AbstractPolytope; ...)

Plot a 2D polytope as the convex hull of its vertices.

Input

• P – polygon or polytope

Examples

julia> using Plots, LazySets;

julia> P = HPolygon([LinearConstraint([1.0, 0.0], 0.6),
                     LinearConstraint([0.0, 1.0], 0.6),
                     LinearConstraint([-1.0, 0.0], -0.4),
                     LinearConstraint([0.0, -1.0], -0.4)]);

julia> plot(P);

This recipe also applies if the polygon is given in vertex representation:

julia> P = VPolygon([[0.6, 0.6], [0.4, 0.6], [0.4, 0.4], [0.6, 0.4]]);

julia> plot(P);

plot_polytopes(Xk::Vector{S}; ...)

Plot an array of 2D polytopes.

Input

• Xk – array of polytopes

Examples

julia> using Plots, LazySets;

julia> P1 = HPolygon([LinearConstraint([1.0, 0.0], 0.6),
                      LinearConstraint([0.0, 1.0], 0.6),
                      LinearConstraint([-1.0, 0.0], -0.4),
                      LinearConstraint([0.0, -1.0], -0.4)]);

julia> P2 = HPolygon([LinearConstraint([2.0, 0.0], 0.6),
                      LinearConstraint([0.0, 2.0], 0.6),
                      LinearConstraint([-2.0, 0.0], -0.4),
                      LinearConstraint([0.0, -2.0], -0.4)]);

julia> plot([P1, P2]);

julia> P1 = VPolygon([[0.6, 0.6], [0.4, 0.6], [0.4, 0.4], [0.6, 0.4]]);

julia> P2 = VPolygon([[0.3, 0.3], [0.2, 0.3], [0.2, 0.2], [0.3, 0.2]]);

julia> plot([P1, P2]);

Notes

It is assumed that the given vector of polytopes is two-dimensional.

AbstractPolygon{N<:Real} <: AbstractPolytope{N}

Abstract type for polygons (i.e., 2D polytopes).

Notes

Every concrete AbstractPolygon must define the following functions:

• tovrep(::AbstractPolygon{N})::VPolygon{N} – transform into V-representation
• tohrep(::AbstractPolygon{N})::S where {S<:AbstractHPolygon{N}} – transform into H-representation

julia> subtypes(AbstractPolygon)
2-element Array{Any,1}:
 AbstractHPolygon
 VPolygon

dim(P::AbstractPolygon)::Int

Return the ambient dimension of a polygon.

Input

• P – polygon

Output

The ambient dimension of the polygon, which is 2.

linear_map(M::AbstractMatrix{N},
           P::AbstractPolyhedron{N};
           check_invertibility::Bool=true,
           cond_tol::Number=DEFAULT_COND_TOL,
           use_inv::Bool=!issparse(M)
           ) where {N<:Real}

Concrete linear map of a polyhedron in constraint representation.

Input

• M – matrix
• P – abstract polyhedron
• check_invertibility – (optional, deault: true) check if the linear map is invertible, in which case this function uses the matrix inverse; if the invertibility check fails, or if this flag is set to false, use the vertex representation to compute the linear map (see below for details)
• cond_tol – (optional) tolerance of matrix condition (used to check whether the matrix is invertible)
• use_inv – (optional, default: false if M is sparse and true otherwise) whether to compute the full left division through inv(M), or to use the left division for each vector; see below

Output

The type of the result is "as close as possible" to the the type of P. Let (m, n) be the size of M, where m ≠ n is allowed for rectangular maps.

To fix the type of the output to something different than the default value, consider post-processing the result of this function with a call to a suitable convert method.

In particular, the output depends on the type of P, on m, and the algorithm that was used:

• If the vertex-based approach was used:

  • If P is a VPolygon and m = 2 then the output is a VPolygon.
  • If P is a VPolytope then the output is a VPolytope.
  • Otherwise, the output is an Interval if m = 1, a VPolygon if m = 2 and a VPolytope in other cases.

• If the invertibility criterion was used:

  • The types of HalfSpace, Hyperplane, Line and AbstractHPolygon are preserved.
  • If P is an AbstractPolytope, then the output is an Interval if m = 1, an HPolygon if m = 2 and an HPolytope in other cases.
  • Otherwise, the output is an HPolyhedron.

Algorithm

This function implements two algorithms for the linear map:

• If the matrix $M$ is invertible (which we check with a sufficient condition), then $y = M x$ implies $x = \text{inv}(M) y$ and we transform the constraint system $A x ≤ b$ to $A \text{inv}(M) y ≤ b$.
• Otherwise, we transform the polyhedron to vertex representation and apply the map to each vertex, returning a polyhedron in vertex representation.

Note that the vertex representation (second approach) is only available if the polyhedron is bounded. Hence we check boundedness first.

To switch off the check for invertibility, set the option check_invertibility=false. If M is not invertible and the polyhedron is unbounded, this function returns an exception.

The option use_inv lets the user control - in case M is invertible - if the full matrix inverse is computed, or only the left division on the normal vectors. Note that this helps as a workaround when M is a sparse matrix, since the inv function is not available for sparse matrices. In this case, either use the option use_inv=false or convert the type of M as in linear_map(Matrix(M), P).

Internally, this function operates at the level of the AbstractPolyhedron interface, but the actual algorithm uses dispatch on the concrete type of P, depending on the algorithm that is used:

• _linear_map_vrep(M, P) if the vertex approach is used
• _linear_map_hrep(M, P, use_inv) if the invertibility criterion is used

New subtypes of the interface should write their own _linear_map_vrep (resp. _linear_map_hrep) for special handling of the linear map; otherwise the fallback implementation for AbstractPolyhedron is used (see below).

AbstractHPolygon{N<:Real} <: AbstractPolygon{N}

Abstract type for polygons in H-representation (i.e., constraints).

Notes

Every concrete AbstractHPolygon must have the following fields:

• constraints::Vector{LinearConstraint{N}} – the constraints

New subtypes should be added to the convert method in order to be convertible.

julia> subtypes(AbstractHPolygon)
2-element Array{Any,1}:
 HPolygon
 HPolygonOpt

an_element(P::AbstractHPolygon{N})::Vector{N} where {N<:Real}

Return some element of a polygon in constraint representation.

Input

• P – polygon in constraint representation

Output

A vertex of the polygon in constraint representation (the first one in the order of the constraints).

∈(x::AbstractVector{N}, P::AbstractHPolygon{N})::Bool where {N<:Real}

Check whether a given 2D point is contained in a polygon in constraint representation.

Input

• x – two-dimensional point/vector
• P – polygon in constraint representation

Output

true iff $x ∈ P$.

Algorithm

This implementation checks if the point lies on the outside of each edge.

rand(::Type{HPOLYGON}; [N]::Type{<:Real}=Float64, [dim]::Int=2,
     [rng]::AbstractRNG=GLOBAL_RNG, [seed]::Union{Int, Nothing}=nothing,
     [num_constraints]::Int=-1
    )::HPOLYGON{N} where {HPOLYGON<:AbstractHPolygon}

Create a random polygon in constraint representation.

Input

• HPOLYGON – type for dispatch
• N – (optional, default: Float64) numeric type
• dim – (optional, default: 2) dimension
• rng – (optional, default: GLOBAL_RNG) random number generator
• seed – (optional, default: nothing) seed for reseeding
• num_constraints – (optional, default: -1) number of constraints of the polygon (must be 3 or bigger; see comment below)

Output

A random polygon in constraint representation.

Algorithm

We create a random polygon in vertex representation and convert it to constraint representation. See rand(::Type{VPolygon}). For non-flat polygons the number of vertices and the number of constraints are identical.

tohrep(P::HPOLYGON)::HPOLYGON where {HPOLYGON<:AbstractHPolygon}

Build a contraint representation of the given polygon.

Input

• P – polygon in constraint representation

Output

The identity, i.e., the same polygon instance.

tovrep(P::AbstractHPolygon{N})::VPolygon{N} where {N<:Real}

Build a vertex representation of the given polygon.

Input

• P – polygon in constraint representation

Output

The same polygon but in vertex representation, a VPolygon.

addconstraint!(P::AbstractHPolygon{N},
               constraint::LinearConstraint{N};
               [linear_search]::Bool=(length(P.constraints) <
                                      BINARY_SEARCH_THRESHOLD),
               [prune]::Bool=true
              )::Nothing where {N<:Real}

Add a linear constraint to a polygon in constraint representation, keeping the constraints sorted by their normal directions.

Input

• P – polygon in constraint representation
• constraint – linear constraint to add
• linear_search – (optional, default: length(constraints) < BINARY_SEARCH_THRESHOLD) flag to choose between linear and binary search
• prune – (optional, default: true) flag for removing redundant constraints in the end

Output

Nothing.

addconstraint!(constraints::Vector{LinearConstraint{N}},
               new_constraint::LinearConstraint{N};
               [linear_search]::Bool=(length(P.constraints) <
                                      BINARY_SEARCH_THRESHOLD),
               [prune]::Bool=true
              )::Nothing where {N<:Real}

Add a linear constraint to a sorted vector of constrains, keeping the constraints sorted by their normal directions.

Input

• constraints – vector of linear constraintspolygon in constraint representation
• new_constraint – linear constraint to add
• linear_search – (optional, default: length(constraints) < BINARY_SEARCH_THRESHOLD) flag to choose between linear and binary search
• prune – (optional, default: true) flag for removing redundant constraints in the end

Output

Nothing.

Algorithm

If prune is active, we check if the new constraint is redundant. If the constraint is not redundant, we perform the same check to the left and to the right until we find the first constraint that is not redundant.

isredundant(cmid::LinearConstraint{N}, cright::LinearConstraint{N},
            cleft::LinearConstraint{N})::Bool where {N<:Real}

Check whether a linear constraint is redundant wrt. two surrounding constraints.

Input

• cmid – linear constraint of concern
• cright – linear constraint to the right (clockwise turn)
• cleft – linear constraint to the left (counter-clockwise turn)

Output

true iff the constraint is redundant.

Algorithm

We first check whether the angle between the surrounding constraints is < 180°, which is a necessary condition (unless the direction is identical to one of the other two constraints). If so, we next check if the angle is 0°, in which case the constraint cmid is redundant unless it is strictly tighter than the other two constraints. If the angle is strictly between 0° and 180°, the constraint cmid is redundant if and only if the vertex defined by the other two constraints lies inside the set defined by cmid.

remove_redundant_constraints!(P::AbstractHPolygon)

Remove all redundant constraints of a polygon in constraint representation.

Input

• P – polygon in constraint representation

Output

The same polygon with all redundant constraints removed.

Notes

Since we only consider bounded polygons and a polygon needs at least three constraints to be bounded, we stop removing redundant constraints if there are three or less constraints left. This means that for non-bounded polygons the result may be unexpected.

Algorithm

We go through all consecutive triples of constraints and check if the one in the middle is redundant. For this we assume that the constraints are sorted.

constraints_list(P::AbstractHPolygon{N})::Vector{LinearConstraint{N}} where {N<:Real}

Return the list of constraints defining a polygon in H-representation.

Input

• P – polygon in H-representation

Output

The list of constraints of the polygon.

vertices_list(P::AbstractHPolygon{N},
              apply_convex_hull::Bool=false,
              check_feasibility::Bool=true
             )::Vector{Vector{N}} where {N<:Real}

Return the list of vertices of a polygon in constraint representation.

Input

• P – polygon in constraint representation
• apply_convex_hull – (optional, default: false) flag to post-process the intersection of constraints with a convex hull
• check_feasibility – (optional, default: true) flag to check whether the polygon was empty (required for correctness in case of empty polygons)

Output

List of vertices.

Algorithm

We compute each vertex as the intersection of consecutive lines defined by the half-spaces. If check_feasibility is active, we then check if the constraints of the polygon were actually feasible (i.e., they pointed in the right direction). For this we compute the average of all vertices and check membership in each constraint.

isbounded(P::AbstractHPolygon, [use_type_assumption]::Bool=true)::Bool

Determine whether a polygon in constraint representation is bounded.

Input

• P – polygon in constraint representation
• use_type_assumption – (optional, default: true) flag for ignoring the type assumption that polygons are bounded

Output

true if use_type_assumption is activated. Otherwise, true iff P is bounded.

Algorithm

If !use_type_assumption, we convert P to an HPolyhedron P2 and then use isbounded(P2).

AbstractCentrallySymmetricPolytope{N<:Real} <: AbstractPolytope{N}

Abstract type for centrally symmetric, polytopic sets. It combines the AbstractCentrallySymmetric and AbstractPolytope interfaces. Such a type combination is necessary as long as Julia does not support multiple inheritance.

Notes

Every concrete AbstractCentrallySymmetricPolytope must define the following functions:

• from AbstractCentrallySymmetric:
  • center(::AbstractCentrallySymmetricPolytope{N})::Vector{N} – return the center point
• from AbstractPolytope:
  • vertices_list(::AbstractCentrallySymmetricPolytope{N})::Vector{Vector{N}} – return a list of all vertices

julia> subtypes(AbstractCentrallySymmetricPolytope)
4-element Array{Any,1}:
 AbstractHyperrectangle
 Ball1
 LineSegment
 Zonotope

dim(P::AbstractCentrallySymmetricPolytope)::Int

Return the ambient dimension of a centrally symmetric, polytopic set.

Input

• P – centrally symmetric, polytopic set

Output

The ambient dimension of the polytopic set.

an_element(P::AbstractCentrallySymmetricPolytope{N})::Vector{N}
    where {N<:Real}

Return some element of a centrally symmetric polytope.

Input

• P – centrally symmetric polytope

Output

The center of the centrally symmetric polytope.

isempty(P::AbstractCentrallySymmetricPolytope)::Bool

Return if a centrally symmetric, polytopic set is empty or not.

Input

• P – centrally symmetric, polytopic set

Output

false.

AbstractHyperrectangle{N<:Real} <: AbstractCentrallySymmetricPolytope{N}

Abstract type for hyperrectangular sets.

Notes

Every concrete AbstractHyperrectangle must define the following functions:

• radius_hyperrectangle(::AbstractHyperrectangle{N})::Vector{N} – return the hyperrectangle's radius, which is a full-dimensional vector
• radius_hyperrectangle(::AbstractHyperrectangle{N}, i::Int)::N – return the hyperrectangle's radius in the i-th dimension

julia> subtypes(AbstractHyperrectangle)
5-element Array{Any,1}:
 AbstractSingleton
 BallInf
 Hyperrectangle
 Interval
 SymmetricIntervalHull

norm(H::AbstractHyperrectangle, [p]::Real=Inf)::Real

Return the norm of a hyperrectangular set.

The norm of a hyperrectangular set is defined as the norm of the enclosing ball, of the given $p$-norm, of minimal volume that is centered in the origin.

Input

• H – hyperrectangular set
• p – (optional, default: Inf) norm

Output

A real number representing the norm.

Algorithm

Recall that the norm is defined as

The last equality holds because the optimum of a convex function over a polytope is attained at one of its vertices.

This implementation uses the fact that the maximum is achieved in the vertex $c + \text{diag}(\text{sign}(c)) r$, for any $p$-norm, hence it suffices to take the $p$-norm of this particular vertex. This statement is proved below. Note that, in particular, there is no need to compute the $p$-norm for each vertex, which can be very expensive.

If $X$ is an axis-aligned hyperrectangle and the $n$-dimensional vectors center and radius of the hyperrectangle are denoted $c$ and $r$ respectively, then reasoning on the $2^n$ vertices we have that:

The function $x ↦ x^p$, $p > 0$, is monotonically increasing and thus the maximum of each term $|c_i + α_i r_i|^p$ is given by $|c_i + \text{sign}(c_i) r_i|^p$ for each $i$. Hence, $x^* := \text{argmax}_{x ∈ X} ‖ x ‖_p$ is the vertex $c + \text{diag}(\text{sign}(c)) r$.

radius(H::AbstractHyperrectangle, [p]::Real=Inf)::Real

Return the radius of a hyperrectangular set.

Input

• H – hyperrectangular set
• p – (optional, default: Inf) norm

Output

A real number representing the radius.

Notes

The radius is defined as the radius of the enclosing ball of the given $p$-norm of minimal volume with the same center. It is the same for all corners of a hyperrectangular set.

σ(d::AbstractVector{N}, H::AbstractHyperrectangle{N}) where {N<:Real}

Return the support vector of a hyperrectangular set in a given direction.

Input

• d – direction
• H – hyperrectangular set

Output

The support vector in the given direction. If the direction has norm zero, the vertex with biggest values is returned.

∈(x::AbstractVector{N}, H::AbstractHyperrectangle{N})::Bool where {N<:Real}

Check whether a given point is contained in a hyperrectangular set.

Input

• x – point/vector
• H – hyperrectangular set

Output

true iff $x ∈ H$.

Algorithm

Let $H$ be an $n$-dimensional hyperrectangular set, $c_i$ and $r_i$ be the box's center and radius and $x_i$ be the vector $x$ in dimension $i$, respectively. Then $x ∈ H$ iff $|c_i - x_i| ≤ r_i$ for all $i=1,…,n$.

vertices_list(H::AbstractHyperrectangle{N})::Vector{Vector{N}} where {N<:Real}

Return the list of vertices of a hyperrectangular set.

Input

• H – hyperrectangular set

Output

A list of vertices.

Notes

For high dimensions, it is preferable to develop a vertex_iterator approach.

constraints_list(H::AbstractHyperrectangle{N})::Vector{LinearConstraint{N}}
    where {N<:Real}

Return the list of constraints of an axis-aligned hyperrectangular set.

Input

• H – hyperrectangular set

Output

A list of linear constraints.

high(H::AbstractHyperrectangle{N})::Vector{N} where {N<:Real}

Return the higher coordinates of a hyperrectangular set.

Input

• H – hyperrectangular set

Output

A vector with the higher coordinates of the hyperrectangular set.

high(H::AbstractHyperrectangle{N}, i::Int)::N where {N<:Real}

Return the higher coordinate of a hyperrectangular set in a given dimension.

Input

• H – hyperrectangular set
• i – dimension of interest

Output

The higher coordinate of the hyperrectangular set in the given dimension.

low(H::AbstractHyperrectangle{N})::Vector{N} where {N<:Real}

Return the lower coordinates of a hyperrectangular set.

Input

• H – hyperrectangular set

Output

A vector with the lower coordinates of the hyperrectangular set.

low(H::AbstractHyperrectangle{N}, i::Int)::N where {N<:Real}

Return the lower coordinate of a hyperrectangular set in a given dimension.

Input

• H – hyperrectangular set
• i – dimension of interest

Output

The lower coordinate of the hyperrectangular set in the given dimension.

split(H::AbstractHyperrectangle{N}, num_blocks::AbstractVector{Int}
     ) where {N<:Real}

Partition a hyperrectangular set into uniform sub-hyperrectangles.

Input

• H – hyperrectangular set
• num_blocks – number of blocks in the partition for each dimension

Output

A list of Hyperrectangles.

AbstractSingleton{N<:Real} <: AbstractHyperrectangle{N}

Abstract type for sets with a single value.

Notes

Every concrete AbstractSingleton must define the following functions:

• element(::AbstractSingleton{N})::Vector{N} – return the single element
• element(::AbstractSingleton{N}, i::Int)::N – return the single element's entry in the i-th dimension

julia> subtypes(AbstractSingleton)
2-element Array{Any,1}:
 Singleton
 ZeroSet

σ(d::AbstractVector{N}, S::AbstractSingleton{N}) where {N<:Real}

Return the support vector of a set with a single value.

Input

• d – direction
• S – set with a single value

Output

The support vector, which is the set's vector itself, irrespective of the given direction.

∈(x::AbstractVector{N}, S::AbstractSingleton{N})::Bool where {N<:Real}

Check whether a given point is contained in a set with a single value.

Input

• x – point/vector
• S – set with a single value

Output

true iff $x ∈ S$.

Notes

This implementation performs an exact comparison, which may be insufficient with floating point computations.

an_element(S::LazySet{N}) where {N<:Real}

Return some element of a convex set.

Input

• S – convex set

Output

An element of a convex set.

an_element(P::AbstractCentrallySymmetricPolytope{N})::Vector{N}
    where {N<:Real}

Return some element of a centrally symmetric polytope.

Input

• P – centrally symmetric polytope

Output

The center of the centrally symmetric polytope.

center(S::AbstractSingleton{N})::Vector{N} where {N<:Real}

Return the center of a set with a single value.

Input

• S – set with a single value

Output

The only element of the set.

vertices_list(S::AbstractSingleton{N})::Vector{Vector{N}} where {N<:Real}

Return the list of vertices of a set with a single value.

Input

• S – set with a single value

Output

A list containing only a single vertex.

radius_hyperrectangle(S::AbstractSingleton{N})::Vector{N} where {N<:Real}

Return the box radius of a set with a single value in every dimension.

Input

• S – set with a single value

Output

The zero vector.

radius_hyperrectangle(S::AbstractSingleton{N}, i::Int)::N where {N<:Real}

Return the box radius of a set with a single value in a given dimension.

Input

• S – set with a single value
• i – dimension of interest

Output

Zero.

high(S::AbstractSingleton{N})::Vector{N} where {N<:Real}

Return the higher coordinates of a set with a single value.

Input

• S – set with a single value

Output

A vector with the higher coordinates of the set with a single value.

high(S::AbstractSingleton{N}, i::Int)::N where {N<:Real}

Return the higher coordinate of a set with a single value in the given dimension.

Input

• S – set with a single value
• i – dimension of interest

Output

The higher coordinate of the set with a single value in the given dimension.

low(S::AbstractSingleton{N})::Vector{N} where {N<:Real}

Return the lower coordinates of a set with a single value.

Input

• S – set with a single value

Output

A vector with the lower coordinates of the set with a single value.

low(S::AbstractSingleton{N}, i::Int)::N where {N<:Real}

Return the lower coordinate of a set with a single value in the given dimension.

Input

• S – set with a single value
• i – dimension of interest

Output

The lower coordinate of the set with a single value in the given dimension.

linear_map(M::AbstractMatrix{N}, S::AbstractSingleton{N}) where {N<:Real}

Concrete linear map of an abstract singleton.

Input

• M – matrix
• S – abstract singleton

Output

The abstract singleton of the same type of $S$ obtained by applying the linear map to the element in $S$.

plot_singleton(X::AbstractSingleton; ...)

Plot a singleton.

Input

• X – singleton, i.e., a one-element set

Examples

julia> using Plots, LazySets;

julia> plot(Singleton([0.5, 1.0]));

plot_singleton(Xk::Vector{S}; ...) where {S<:AbstractSingleton}

Plot a list of singletons.

Input

• Xk – list of singletons, i.e., a vector of one-element sets

Examples

julia> using Plots, LazySets;

julia> plot([Singleton([0.0, 0.0]), Singleton([1., 0]), Singleton([0.5, .5])]);

Three-dimensional singletons can be plotted as well:

julia> using Plots, LazySets;

julia> a, b, c = zeros(3), [1.0, 0, 0], [0.0, 1., 0];

julia> plot([Singleton(a), Singleton(b), Singleton(c)]);