Reach Set Approximation through Decomposition with Low-dimensional Sets and High-dimensional Matrices

Publication

Reach Set Approximation through Decomposition with Low-dimensional Sets and High-dimensional Matrices. Sergiy Bogomolov, Marcelo Forets, Goran Frehse, Frédéric Viry, Andreas Podelski and Christian Schilling (2018) HSCC'18 Proceedings of the 21st International Conference on Hybrid Systems: Computation and Control: 41–50. See the ACM Digital Library link, or the arXiv: 1801.09526.

Abstract

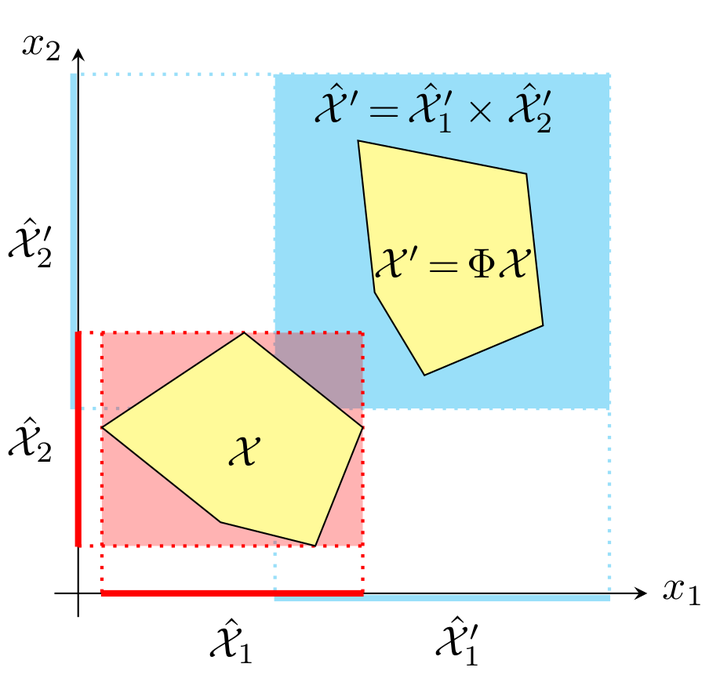
Approximating the set of reachable states of a dynamical system is an algorithmic yet mathematically rigorous way to reason about its safety. Although progress has been made in the development of efficient algorithms for affine dynamical systems, available algorithms still lack scalability to ensure their wide adoption in the industrial setting. While modern linear algebra packages are efficient for matrices with tens of thousands of dimensions, set-based image computations are limited to a few hundred. We propose to decompose reach set computations such that set operations are performed in low dimensions, while matrix operations like exponentiation are carried out in the full dimension. Our method is applicable both in dense and discrete-time settings. For a set of standard benchmarks, it shows a speed-up of up to two orders of magnitude compared to the respective state-of-the-art tools, with only modest losses in accuracy. For the dense-time case, we show an experiment with more than 10,000 variables, roughly two orders of magnitude higher than possible with previous approaches.

Contributions

We present a new method to solve the reachability problem for affine dynamical systems with nondeterministic inputs and experimentally show that it is highly scalable under modest loss of accuracy.

More precisely:

• We provide a new decomposition approach to solve the set-based recurrence:

$$ \mathcal{X}(k+1) = \Phi \mathcal{X}(k) \oplus \mathcal{V}(k),\qquad k = 0, 1,\ldots, N $$

• We analyze the approximation error.

• We address both the dense time and the discrete time reach- ability problem for general linear time-invariant systems.

• We implement our approach efficiently and demonstrate its scalability on real engineering benchmarks. The tool, source code, and benchmark scripts are publicly available.

How to cite

@inproceedings{bogomolov2018reach,
  title={Reach set approximation through decomposition with low-dimensional sets and high-dimensional matrices},
  author={Bogomolov, Sergiy and Forets, Marcelo and Frehse, Goran and Viry, Fr{\'e}d{\'e}ric and Podelski, Andreas and Schilling, Christian},
  booktitle={Proceedings of the 21st International Conference on Hybrid Systems: Computation and Control (part of CPS Week)},
  pages={41--50},
  year={2018}
}