Reachability analysis of linear hybrid systems via block decomposition

Publication

Abstract

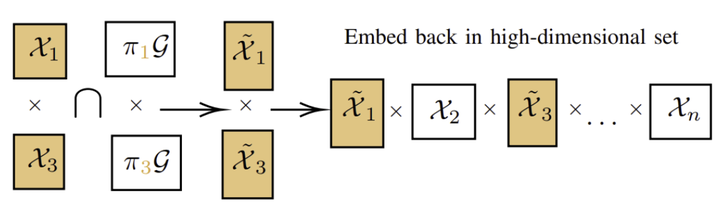
Reachability analysis aims at identifying states reachable by a system within a given time horizon. This task is known to be computationally expensive for linear hybrid systems. Reachability analysis works by iteratively applying continuous and discrete post operators to compute states reachable according to continuous and discrete dynamics, respectively. In this article, we enhance both of these operators and make sure that most of the involved computations are performed in low-dimensional state space. In particular, we improve the continuous-post operator by performing computations in high-dimensional state space only for time intervals relevant for the subsequent application of the discrete-post operator. Furthermore, the new discrete-post operator performs low-dimensional computations by leveraging the structure of the guard and assignment of a considered transition. We illustrate the potential of our approach on a number of challenging benchmarks.

Contributions

Presentation

• Presentation slides (pdf) are available here.

• The recording for EMSOFT'20 is available here.

How to cite

@article{forets2020efficient,
  title={Efficient reachability analysis of parametric linear hybrid systems with time-triggered transitions},
  author={Forets, Marcelo and Freire, Daniel and Schilling, Christian},
  journal={arXiv preprint arXiv:2006.12325},
  year={2020}
}