Set Interfaces

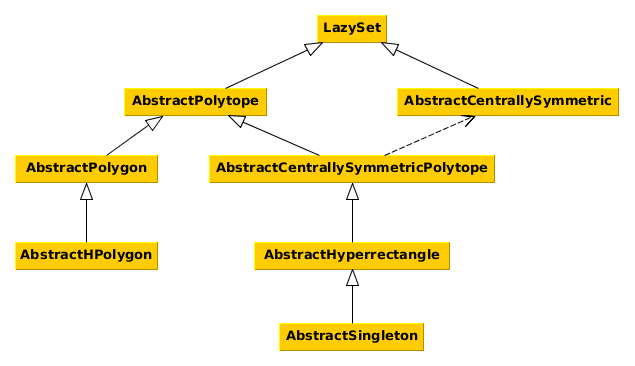
LazySet{N}

Abstract type for convex sets, i.e., sets characterized by a (possibly infinite) intersection of halfspaces, or equivalently, sets $S$ such that for any two elements $x, y ∈ S$ and $0 ≤ λ ≤ 1$ it holds that $λ·x + (1-λ)·y ∈ S$.

Notes

LazySet types should be parameterized with a type N, typically N<:Real, for using different numeric types.

Every concrete LazySet must define the following functions:

• σ(d::AbstractVector{N}, S::LazySet{N}) where {N<:Real} – the support vector of S in a given direction d; note that the numeric type N of d and S must be identical; for some set types N may be more restrictive than Real
• dim(S::LazySet)::Int – the ambient dimension of S

julia> subtypes(LazySet)
19-element Array{Any,1}:
 AbstractCentrallySymmetric
 AbstractPolytope
 CacheMinkowskiSum
 CartesianProduct
 CartesianProductArray
 ConvexHull
 ConvexHullArray
 EmptySet
 ExponentialMap
 ExponentialProjectionMap
 HPolyhedron
 Hyperplane
 Intersection
 IntersectionArray
 HalfSpace
 Line
 LinearMap
 MinkowskiSum
 MinkowskiSumArray

support_vector

Alias for the support vector σ.

ρ(d::AbstractVector{N}, S::LazySet{N})::N where {N<:Real}

Evaluate the support function of a set in a given direction.

Input

• d – direction
• S – convex set

Output

The support function of the set S for the direction d.

Notes

The numeric type of the direction and the set must be identical.

support_function

Alias for the support function ρ.

norm(S::LazySet, [p]::Real=Inf)

Return the norm of a convex set. It is the norm of the enclosing ball (of the given $p$-norm) of minimal volume that is centered in the origin.

Input

• S – convex set
• p – (optional, default: Inf) norm

Output

A real number representing the norm.

radius(S::LazySet, [p]::Real=Inf)

Return the radius of a convex set. It is the radius of the enclosing ball (of the given $p$-norm) of minimal volume with the same center.

Input

• S – convex set
• p – (optional, default: Inf) norm

Output

A real number representing the radius.

diameter(S::LazySet, [p]::Real=Inf)

Return the diameter of a convex set. It is the maximum distance between any two elements of the set, or, equivalently, the diameter of the enclosing ball (of the given $p$-norm) of minimal volume with the same center.

Input

• S – convex set
• p – (optional, default: Inf) norm

Output

A real number representing the diameter.

an_element(S::LazySet{N}) where {N<:Real}

Return some element of a convex set.

Input

• S – convex set

Output

An element of a convex set.

==(X::LazySet, Y::LazySet)

Return whether two LazySets of the same type are exactly equal by recursively comparing their fields until a mismatch is found.

Input

• X – any LazySet
• Y – another LazySet of the same type as X

Output

• true iff X is equal to Y.

Notes

The check is purely syntactic and the sets need to have the same base type. I.e. X::VPolytope == Y::HPolytope returns false even if X and Y represent the same polytope. However X::HPolytope{Int64} == Y::HPolytope{Float64} is a valid comparison.

Examples

julia> HalfSpace([1], 1) == HalfSpace([1], 1)
true

julia> HalfSpace([1], 1) == HalfSpace([1.0], 1.0)
true

julia> Ball1([0.], 1.) == Ball2([0.], 1.)
false

CompactSet

An alias for compact set types.

Notes

Most lazy operations are not captured by this alias because whether their result is compact or not depends on the argument(s).

NonCompactSet

An alias for non-compact set types.

Notes

Most lazy operations are not captured by this alias because whether their result is non-compact or not depends on the argument(s).

AbstractCentrallySymmetric{N<:Real} <: LazySet{N}

Abstract type for centrally symmetric sets.

Notes

Every concrete AbstractCentrallySymmetric must define the following functions:

• center(::AbstractCentrallySymmetric{N})::Vector{N} – return the center point

julia> subtypes(AbstractCentrallySymmetric)
3-element Array{Any,1}:
 Ball2
 Ballp
 Ellipsoid

dim(S::AbstractCentrallySymmetric)::Int

Return the ambient dimension of a centrally symmetric set.

Input

• S – set

Output

The ambient dimension of the set.

an_element(S::AbstractCentrallySymmetric{N})::Vector{N} where {N<:Real}

Return some element of a centrally symmetric set.

Input

• S – centrally symmetric set

Output

The center of the centrally symmetric set.

isempty(S::AbstractCentrallySymmetric)::Bool

Return if a centrally symmetric set is empty or not.

Input

• S – centrally symmetric set

Output

false.

AbstractPolytope{N<:Real} <: LazySet{N}

Abstract type for polytopic sets, i.e., sets with finitely many flat facets, or equivalently, sets defined as an intersection of a finite number of halfspaces, or equivalently, sets with finitely many vertices.

Notes

Every concrete AbstractPolytope must define the following functions:

• constraints_list(::AbstractPolytope{N})::Vector{LinearConstraint{N}} – return a list of all facet constraints
• vertices_list(::AbstractPolytope{N})::Vector{Vector{N}} – return a list of all vertices

julia> subtypes(AbstractPolytope)
4-element Array{Any,1}:
 AbstractCentrallySymmetricPolytope
 AbstractPolygon
 HPolytope
 VPolytope

singleton_list(P::AbstractPolytope{N})::Vector{Singleton{N}} where {N<:Real}

Return the vertices of a polytopic set as a list of singletons.

Input

• P – a polytopic set

Output

List containing a singleton for each vertex.

linear_map(M::AbstractMatrix, P::AbstractPolytope{N};
           output_type::Type{<:LazySet}=VPolytope{N}) where {N<:Real}

Concrete linear map of an abstract polytype.

Input

• M – matrix
• P – abstract polytype
• output_type – (optional, default: VPolytope) type of the result

Output

A set of type output_type.

Algorithm

The linear map $M$ is applied to each vertex of the given set $P$, obtaining a polytope in V-representation. Since some set representations (e.g. axis-aligned hyperrectangles) are not closed under linear maps, the default output is a VPolytope. If an output_type is given, the corresponding convert method is invoked.

isempty(P::AbstractPolytope{N})::Bool where {N<:Real}

Determine whether a polytope is empty.

Input

• P – abstract polytope

Output

true if the given polytope contains no vertices, and false otherwise.

Algorithm

This algorithm checks whether the vertices_list of the given polytope is empty or not.

AbstractPolygon{N<:Real} <: AbstractPolytope{N}

Abstract type for polygons (i.e., 2D polytopes).

Notes

Every concrete AbstractPolygon must define the following functions:

• tovrep(::AbstractPolygon{N})::VPolygon{N} – transform into V-representation
• tohrep(::AbstractPolygon{N})::AbstractHPolygon{N} – transform into H-representation

julia> subtypes(AbstractPolygon)
2-element Array{Any,1}:
 AbstractHPolygon
 VPolygon

dim(P::AbstractPolygon)::Int

Return the ambient dimension of a polygon.

Input

• P – polygon

Output

The ambient dimension of the polygon, which is 2.

linear_map(M::AbstractMatrix, P::AbstractPolygon{N};
           output_type::Type{<:LazySet}=typeof(P)) where {N}

Concrete linear map of an abstract polygon.

Input

• M – matrix
• P – abstract polygon
• output_type – (optional, default: type of P) type of the result

Output

A set of type output_type.

Algorithm

The linear map $M$ is applied to each vertex of the given set $P$, obtaining a polygon in V-representation. Since polygons are closed under linear map, by default $MP$ is converted to the concrete type of $P$. If an output_type is given, the corresponding convert method is invoked.

AbstractHPolygon{N<:Real} <: AbstractPolygon{N}

Abstract type for polygons in H-representation (i.e., constraints).

Notes

Every concrete AbstractHPolygon must have the following fields:

• constraints::Vector{LinearConstraint{N}} – the constraints

New subtypes should be added to the convert method in order to be convertible.

julia> subtypes(AbstractHPolygon)
2-element Array{Any,1}:
 HPolygon
 HPolygonOpt

an_element(P::AbstractHPolygon{N})::Vector{N} where {N<:Real}

Return some element of a polygon in constraint representation.

Input

• P – polygon in constraint representation

Output

A vertex of the polygon in constraint representation (the first one in the order of the constraints).

∈(x::AbstractVector{N}, P::AbstractHPolygon{N})::Bool where {N<:Real}

Check whether a given 2D point is contained in a polygon in constraint representation.

Input

• x – two-dimensional point/vector
• P – polygon in constraint representation

Output

true iff $x ∈ P$.

Algorithm

This implementation checks if the point lies on the outside of each edge.

vertices_list(P::AbstractHPolygon{N},
              apply_convex_hull::Bool=false
             )::Vector{Vector{N}} where {N<:Real}

Return the list of vertices of a polygon in constraint representation.

Input

• P – polygon in constraint representation
• apply_convex_hull – (optional, default: false) to post process or not the intersection of constraints with a convex hull

Output

List of vertices.

tohrep(P::AbstractHPolygon{N})::AbstractHPolygon{N} where {N<:Real}

Build a contraint representation of the given polygon.

Input

• P – polygon in constraint representation

Output

The identity, i.e., the same polygon instance.

tohrep(P::HPoly{N}) where {N}

Return a constraint representation of the given polyhedron in constraint representation (no-op).

Input

• P – polyhedron in constraint representation

Output

The same polyhedron instance.

tohrep(P::VPolygon{N}, ::Type{HPOLYGON}=HPolygon
      )::AbstractHPolygon{N} where {N<:Real, HPOLYGON<:AbstractHPolygon}

Build a constraint representation of the given polygon.

Input

• P – polygon in vertex representation
• HPOLYGON – (optional, default: HPolygon) type of target polygon

Output

The same polygon but in constraint representation, an AbstractHPolygon.

Algorithm

The algorithms consists of adding an edge for each consecutive pair of vertices. Since the vertices are already ordered in counter-clockwise fashion (CWW), the constraints will be sorted automatically (CCW) if we start with the first edge between the first and second vertex.

tohrep(P::VPolytope{N}; [backend]=default_polyhedra_backend(P, N)) where {N}

Transform a polytope in V-representation to a polytope in H-representation.

Input

• P – polytope in vertex representation
• backend – (optional, default: default_polyhedra_backend(P, N)) the polyhedral computations backend, see Polyhedra's documentation for further information

Output

The HPolytope which is the constraint representation of the given polytope in vertex representation.

tovrep(P::AbstractHPolygon{N})::VPolygon{N} where {N<:Real}

Build a vertex representation of the given polygon.

Input

• P – polygon in constraint representation

Output

The same polygon but in vertex representation, a VPolygon.

tovrep(P::HPoly{N};
      [backend]=default_polyhedra_backend(P, N)) where {N}

Transform a polyhedron in H-representation to a polytope in V-representation.

Input

• P – polyhedron in constraint representation
• backend – (optional, default: default_polyhedra_backend(P, N)) the polyhedral computations backend

Output

The VPolytope which is the vertex representation of the given polyhedron in constraint representation.

Notes

For further information on the supported backends see Polyhedra's documentation.

addconstraint!(P::AbstractHPolygon{N},
               constraint::LinearConstraint{N};
               [linear_search]::Bool=(
                length(P.constraints) < BINARY_SEARCH_THRESHOLD)
              )::Nothing where {N<:Real}

Add a linear constraint to a polygon in constraint representation, keeping the constraints sorted by their normal directions.

Input

• P – polygon in constraint representation
• constraint – linear constraint to add

Output

Nothing.

constraints_list(P::AbstractHPolygon{N})::Vector{LinearConstraint{N}} where {N<:Real}

Return the list of constraints defining a polygon in H-representation.

Input

• P – polygon in H-representation

Output

The list of constraints of the polygon.

AbstractCentrallySymmetricPolytope{N<:Real} <: AbstractPolytope{N}

Abstract type for centrally symmetric, polytopic sets. It combines the AbstractCentrallySymmetric and AbstractPolytope interfaces. Such a type combination is necessary as long as Julia does not support multiple inheritance.

Notes

Every concrete AbstractCentrallySymmetricPolytope must define the following functions:

• from AbstractCentrallySymmetric:
  • center(::AbstractCentrallySymmetricPolytope{N})::Vector{N} – return the center point
• from AbstractPolytope:
  • vertices_list(::AbstractCentrallySymmetricPolytope{N})::Vector{Vector{N}} – return a list of all vertices

julia> subtypes(AbstractCentrallySymmetricPolytope)
4-element Array{Any,1}:
 AbstractHyperrectangle
 Ball1
 LineSegment
 Zonotope

dim(P::AbstractCentrallySymmetricPolytope)::Int

Return the ambient dimension of a centrally symmetric, polytopic set.

Input

• P – centrally symmetric, polytopic set

Output

The ambient dimension of the polytopic set.

an_element(P::AbstractCentrallySymmetricPolytope{N})::Vector{N}
    where {N<:Real}

Return some element of a centrally symmetric polytope.

Input

• P – centrally symmetric polytope

Output

The center of the centrally symmetric polytope.

isempty(P::AbstractCentrallySymmetricPolytope)::Bool

Return if a centrally symmetric, polytopic set is empty or not.

Input

• P – centrally symmetric, polytopic set

Output

false.

AbstractHyperrectangle{N<:Real} <: AbstractCentrallySymmetricPolytope{N}

Abstract type for hyperrectangular sets.

Notes

Every concrete AbstractHyperrectangle must define the following functions:

• radius_hyperrectangle(::AbstractHyperrectangle{N})::Vector{N} – return the hyperrectangle's radius, which is a full-dimensional vector
• radius_hyperrectangle(::AbstractHyperrectangle{N}, i::Int)::N – return the hyperrectangle's radius in the i-th dimension

julia> subtypes(AbstractHyperrectangle)
5-element Array{Any,1}:
 AbstractSingleton
 BallInf
 Hyperrectangle
 Interval
 SymmetricIntervalHull

norm(S::LazySet, [p]::Real=Inf)

Return the norm of a convex set. It is the norm of the enclosing ball (of the given $p$-norm) of minimal volume that is centered in the origin.

Input

• S – convex set
• p – (optional, default: Inf) norm

Output

A real number representing the norm.

norm(H::AbstractHyperrectangle, [p]::Real=Inf)::Real

Return the norm of a hyperrectangular set.

The norm of a hyperrectangular set is defined as the norm of the enclosing ball, of the given $p$-norm, of minimal volume that is centered in the origin.

Input

• H – hyperrectangular set
• p – (optional, default: Inf) norm

Output

A real number representing the norm.

Algorithm

Recall that the norm is defined as

The last equality holds because the optimum of a convex function over a polytope is attained at one of its vertices.

This implementation uses the fact that the maximum is achieved in the vertex $c + \text{diag}(\text{sign}(c)) r$, for any $p$-norm, hence it suffices to take the $p$-norm of this particular vertex. This statement is proved below. Note that, in particular, there is no need to compute the $p$-norm for each vertex, which can be very expensive.

If $X$ is an axis-aligned hyperrectangle and the $n$-dimensional vectors center and radius of the hyperrectangle are denoted $c$ and $r$ respectively, then reasoning on the $2^n$ vertices we have that:

The function $x ↦ x^p$, $p > 0$, is monotonically increasing and thus the maximum of each term $|c_i + α_i r_i|^p$ is given by $|c_i + \text{sign}(c_i) r_i|^p$ for each $i$. Hence, $x^* := \text{argmax}_{x ∈ X} ‖ x ‖_p$ is the vertex $c + \text{diag}(\text{sign}(c)) r$.

radius(S::LazySet, [p]::Real=Inf)

Return the radius of a convex set. It is the radius of the enclosing ball (of the given $p$-norm) of minimal volume with the same center.

Input

• S – convex set
• p – (optional, default: Inf) norm

Output

A real number representing the radius.

radius(H::AbstractHyperrectangle, [p]::Real=Inf)::Real

Return the radius of a hyperrectangular set.

Input

• H – hyperrectangular set
• p – (optional, default: Inf) norm

Output

A real number representing the radius.

Notes

The radius is defined as the radius of the enclosing ball of the given $p$-norm of minimal volume with the same center. It is the same for all corners of a hyperrectangular set.

σ(d::AbstractVector{N}, H::AbstractHyperrectangle{N}) where {N<:Real}

Return the support vector of a hyperrectangular set in a given direction.

Input

• d – direction
• H – hyperrectangular set

Output

The support vector in the given direction. If the direction has norm zero, the vertex with biggest values is returned.

∈(x::AbstractVector{N}, H::AbstractHyperrectangle{N})::Bool where {N<:Real}

Check whether a given point is contained in a hyperrectangular set.

Input

• x – point/vector
• H – hyperrectangular set

Output

true iff $x ∈ H$.

Algorithm

Let $H$ be an $n$-dimensional hyperrectangular set, $c_i$ and $r_i$ be the box's center and radius and $x_i$ be the vector $x$ in dimension $i$, respectively. Then $x ∈ H$ iff $|c_i - x_i| ≤ r_i$ for all $i=1,…,n$.

vertices_list(H::AbstractHyperrectangle{N})::Vector{Vector{N}} where {N<:Real}

Return the list of vertices of a hyperrectangular set.

Input

• H – hyperrectangular set

Output

A list of vertices.

Notes

For high dimensions, it is preferable to develop a vertex_iterator approach.

constraints_list(H::AbstractHyperrectangle{N})::Vector{LinearConstraint{N}}
    where {N<:Real}

Return the list of constraints of an axis-aligned hyperrectangular set.

Input

• H – hyperrectangular set

Output

A list of linear constraints.

high(H::AbstractHyperrectangle{N})::Vector{N} where {N<:Real}

Return the higher coordinates of a hyperrectangular set.

Input

• H – hyperrectangular set

Output

A vector with the higher coordinates of the hyperrectangular set.

low(H::AbstractHyperrectangle{N})::Vector{N} where {N<:Real}

Return the lower coordinates of a hyperrectangular set.

Input

• H – hyperrectangular set

Output

A vector with the lower coordinates of the hyperrectangular set.

AbstractSingleton{N<:Real} <: AbstractHyperrectangle{N}

Abstract type for sets with a single value.

Notes

Every concrete AbstractSingleton must define the following functions:

• element(::AbstractSingleton{N})::Vector{N} – return the single element
• element(::AbstractSingleton{N}, i::Int)::N – return the single element's entry in the i-th dimension

julia> subtypes(AbstractSingleton)
2-element Array{Any,1}:
 Singleton
 ZeroSet

σ(d::AbstractVector{N}, S::AbstractSingleton{N}) where {N<:Real}

Return the support vector of a set with a single value.

Input

• d – direction
• S – set with a single value

Output

The support vector, which is the set's vector itself, irrespective of the given direction.

∈(x::AbstractVector{N}, S::AbstractSingleton{N})::Bool where {N<:Real}

Check whether a given point is contained in a set with a single value.

Input

• x – point/vector
• S – set with a single value

Output

true iff $x ∈ S$.

Notes

This implementation performs an exact comparison, which may be insufficient with floating point computations.

an_element(S::LazySet{N}) where {N<:Real}

Return some element of a convex set.

Input

• S – convex set

Output

An element of a convex set.

an_element(P::AbstractCentrallySymmetricPolytope{N})::Vector{N}
    where {N<:Real}

Return some element of a centrally symmetric polytope.

Input

• P – centrally symmetric polytope

Output

The center of the centrally symmetric polytope.

center(S::AbstractSingleton{N})::Vector{N} where {N<:Real}

Return the center of a set with a single value.

Input

• S – set with a single value

Output

The only element of the set.

vertices_list(S::AbstractSingleton{N})::Vector{Vector{N}} where {N<:Real}

Return the list of vertices of a set with a single value.

Input

• S – set with a single value

Output

A list containing only a single vertex.

radius_hyperrectangle(S::AbstractSingleton{N})::Vector{N} where {N<:Real}

Return the box radius of a set with a single value in every dimension.

Input

• S – set with a single value

Output

The zero vector.

radius_hyperrectangle(S::AbstractSingleton{N}, i::Int)::N where {N<:Real}

Return the box radius of a set with a single value in a given dimension.

Input

• S – set with a single value

Output

Zero.

linear_map(M::AbstractMatrix, S::AbstractSingleton{N}) where {N<:Real}

Concrete linear map of an abstract singleton.

Input

• M – matrix
• S – abstract singleton

Output

The abstract singleton of the same type of $S$ obtained by applying the linear map to the element in $S$.