Set Interfaces

Set Interfaces

This section of the manual describes the interfaces for different set types. Every set that fits the description of an interface should also implement it. This helps in several ways:

The interface functions are outlined in the interface documentation. See Common Set Representations for implementations of the interfaces.

Note

The naming convention is such that all interface names (with the exception of the main abstract type LazySet) should be preceded by Abstract.

The following diagram shows the interface hierarchy.

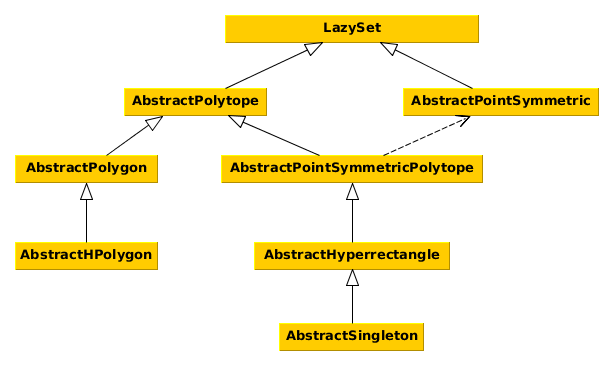
../assets/interfaces.png

LazySet

Every convex set in this library implements this interface.

LazySets.LazySet — Type.
LazySet{N}

Abstract type for convex sets, i.e., sets characterized by a (possibly infinite) intersection of halfspaces, or equivalently, sets $S$ such that for any two elements $x, y ∈ S$ and $0 ≤ λ ≤ 1$ it holds that $λ·x + (1-λ)·y ∈ S$.

Notes

LazySet types should be parameterized with a type N, typically N<:Real, for using different numeric types.

Every concrete LazySet must define the following functions:

  • σ(d::AbstractVector{N}, S::LazySet{N}) where {N<:Real} – the support vector of S in a given direction d; note that the numeric type N of d and S must be identical; for some set types N may be more restrictive than Real

  • dim(S::LazySet)::Int – the ambient dimension of S

julia> subtypes(LazySet)
18-element Array{Any,1}:
 AbstractPointSymmetric
 AbstractPolytope
 CacheMinkowskiSum
 CartesianProduct
 CartesianProductArray
 ConvexHull
 ConvexHullArray
 EmptySet
 ExponentialMap
 ExponentialProjectionMap
 HalfSpace
 Hyperplane
 Intersection
 IntersectionArray
 Line
 LinearMap
 MinkowskiSum
 MinkowskiSumArray
source

Support function and support vector

Every LazySet type must define a function σ to compute the support vector.

LazySets.support_vector — Function.
support_vector

Alias for the support vector σ.

source
LazySets.ρ — Method.
ρ(d::AbstractVector{N}, S::LazySet{N})::N where {N<:Real}

Evaluate the support function of a set in a given direction.

Input

  • d – direction

  • S – convex set

Output

The support function of the set S for the direction d.

Notes

The numeric type of the direction and the set must be identical.

source
LazySets.support_function — Function.
support_function

Alias for the support function ρ.

source

Other globally defined set functions

Base.LinAlg.norm — Method.
norm(S::LazySet, [p]::Real=Inf)

Return the norm of a convex set. It is the norm of the enclosing ball (of the given $p$-norm) of minimal volume that is centered in the origin.

Input

  • S – convex set

  • p – (optional, default: Inf) norm

Output

A real number representing the norm.

source
LazySets.radius — Method.
radius(S::LazySet, [p]::Real=Inf)

Return the radius of a convex set. It is the radius of the enclosing ball (of the given $p$-norm) of minimal volume with the same center.

Input

  • S – convex set

  • p – (optional, default: Inf) norm

Output

A real number representing the radius.

source
LazySets.diameter — Method.
diameter(S::LazySet, [p]::Real=Inf)

Return the diameter of a convex set. It is the maximum distance between any two elements of the set, or, equivalently, the diameter of the enclosing ball (of the given $p$-norm) of minimal volume with the same center.

Input

  • S – convex set

  • p – (optional, default: Inf) norm

Output

A real number representing the diameter.

source
LazySets.an_element — Method.
an_element(S::LazySet{N}) where {N<:Real}

Return some element of a convex set.

Input

  • S – convex set

Output

An element of a convex set.

source

Point symmetric set

Point symmetric sets such as balls of different norms are characterized by a center. Note that there is a special interface combination Point symmetric polytope.

LazySets.AbstractPointSymmetric — Type.
AbstractPointSymmetric{N<:Real} <: LazySet{N}

Abstract type for point symmetric sets.

Notes

Every concrete AbstractPointSymmetric must define the following functions:

  • center(::AbstractPointSymmetric{N})::Vector{N} – return the center point

julia> subtypes(AbstractPointSymmetric)
3-element Array{Any,1}:
 Ball2
 Ballp
 Ellipsoid
source

This interface defines the following functions:

LazySets.dim — Method.
dim(S::AbstractPointSymmetric)::Int

Return the ambient dimension of a point symmetric set.

Input

  • S – set

Output

The ambient dimension of the set.

source
LazySets.an_element — Method.
an_element(S::AbstractPointSymmetric{N})::Vector{N} where {N<:Real}

Return some element of a point symmetric set.

Input

  • S – point symmetric set

Output

The center of the point symmetric set.

source

Polytope

A polytope has finitely many vertices (V-representation) resp. facets (H-representation). Note that there is a special interface combination Point symmetric polytope.

LazySets.AbstractPolytope — Type.
AbstractPolytope{N<:Real} <: LazySet{N}

Abstract type for polytopic sets, i.e., sets with finitely many flat facets, or equivalently, sets defined as an intersection of a finite number of halfspaces, or equivalently, sets with finitely many vertices.

Notes

Every concrete AbstractPolytope must define the following functions:

  • vertices_list(::AbstractPolytope{N})::Vector{Vector{N}} – return a list of all vertices

julia> subtypes(AbstractPolytope)
4-element Array{Any,1}:
 AbstractPointSymmetricPolytope
 AbstractPolygon
 HPolytope
 VPolytope
source

This interface defines the following functions:

LazySets.singleton_list — Method.
singleton_list(P::AbstractPolytope{N})::Vector{Singleton{N}} where {N<:Real}

Return the vertices of a polytopic as a list of singletons.

Input

  • P – a polytopic set

Output

List containing a singleton for each vertex.

source
LazySets.linear_map — Method.
linear_map(M::AbstractMatrix, P::AbstractPolytope{N}) where {N<:Real}

Concrete linear map of an abstract polytype.

Input

  • M – matrix

  • P – abstract polytype

Output

The polytope in V-representation obtained by applying the linear map $M$ to the set $P$. If the given polytope is two-dimensional, a polygon instead of a general polytope is returned.

source

Polygon

A polygon is a two-dimensional polytope.

LazySets.AbstractPolygon — Type.
AbstractPolygon{N<:Real} <: AbstractPolytope{N}

Abstract type for polygons (i.e., 2D polytopes).

Notes

Every concrete AbstractPolygon must define the following functions:

  • tovrep(::AbstractPolygon{N})::VPolygon{N} – transform into V-representation

  • tohrep(::AbstractPolygon{N})::AbstractHPolygon{N} – transform into H-representation

julia> subtypes(AbstractPolygon)
2-element Array{Any,1}:
 AbstractHPolygon
 VPolygon
source

This interface defines the following functions:

LazySets.dim — Method.
dim(P::AbstractPolygon)::Int

Return the ambient dimension of a polygon.

Input

  • P – polygon

Output

The ambient dimension of the polygon, which is 2.

source

HPolygon

An HPolygon is a polygon in H-representation (or constraint representation).

LazySets.AbstractHPolygon — Type.
AbstractHPolygon{N<:Real} <: AbstractPolygon{N}

Abstract type for polygons in H-representation (i.e., constraints).

Notes

Every concrete AbstractHPolygon must have the following fields:

  • constraints::Vector{LinearConstraint{N}} – the constraints

New subtypes should be added to the convert method in order to be convertible.

julia> subtypes(AbstractHPolygon)
2-element Array{Any,1}:
 HPolygon
 HPolygonOpt
source

This interface defines the following functions:

LazySets.an_element — Method.
an_element(P::AbstractHPolygon{N})::Vector{N} where {N<:Real}

Return some element of a polygon in constraint representation.

Input

  • P – polygon in constraint representation

Output

A vertex of the polygon in constraint representation (the first one in the order of the constraints).

source
Base.:∈ — Method.
∈(x::AbstractVector{N}, P::AbstractHPolygon{N})::Bool where {N<:Real}

Check whether a given 2D point is contained in a polygon in constraint representation.

Input

  • x – two-dimensional point/vector

  • P – polygon in constraint representation

Output

true iff $x ∈ P$.

Algorithm

This implementation checks if the point lies on the outside of each edge.

source
LazySets.vertices_list — Method.
vertices_list(P::AbstractHPolygon{N},
              apply_convex_hull::Bool=false
             )::Vector{Vector{N}} where {N<:Real}

Return the list of vertices of a polygon in constraint representation.

Input

  • P – polygon in constraint representation

  • apply_convex_hull – (optional, default: false) to post process or not the intersection of constraints with a convex hull

Output

List of vertices.

source
LazySets.tohrep — Method.
tohrep(P::AbstractHPolygon{N})::AbstractHPolygon{N} where {N<:Real}

Build a contraint representation of the given polygon.

Input

  • P – polygon in constraint representation

Output

The identity, i.e., the same polygon instance.

source
tohrep(P::VPolygon{N}, ::Type{HPOLYGON}=HPolygon
      )::AbstractHPolygon{N} where {N<:Real, HPOLYGON<:AbstractHPolygon}

Build a constraint representation of the given polygon.

Input

  • P – polygon in vertex representation

  • HPOLYGON – (optional, default: HPolygon) type of target polygon

Output

The same polygon but in constraint representation, an AbstractHPolygon.

Algorithm

The algorithms consists of adding an edge for each consecutive pair of vertices. Since the vertices are already ordered in counter-clockwise fashion (CWW), the constraints will be sorted automatically (CCW) if we start with the first edge between the first and second vertex.

source
LazySets.tovrep — Method.
tovrep(P::AbstractHPolygon{N})::VPolygon{N} where {N<:Real}

Build a vertex representation of the given polygon.

Input

  • P – polygon in constraint representation

Output

The same polygon but in vertex representation, a VPolygon.

source
LazySets.addconstraint! — Method.
addconstraint!(P::AbstractHPolygon{N},
               constraint::LinearConstraint{N};
               [linear_search]::Bool=(
                length(P.constraints) < BINARY_SEARCH_THRESHOLD)
              )::Nothing where {N<:Real}

Add a linear constraint to a polygon in constraint representation, keeping the constraints sorted by their normal directions.

Input

  • P – polygon in constraint representation

  • constraint – linear constraint to add

Output

Nothing.

source
LazySets.constraints_list — Method.
constraints_list(P::AbstractHPolygon{N})::Vector{LinearConstraint{N}} where {N<:Real}

Return the list of constraints defining a polygon in H-representation.

Input

  • P – polygon in H-representation

Output

The list of constraints of the polygon.

source

Point symmetric polytope

A point symmetric polytope is a combination of two other interfaces: Point symmetric set and Polytope.

LazySets.AbstractPointSymmetricPolytope — Type.
AbstractPointSymmetricPolytope{N<:Real} <: AbstractPolytope{N}

Abstract type for point symmetric, polytopic sets. It combines the AbstractPointSymmetric and AbstractPolytope interfaces. Such a type combination is necessary as long as Julia does not support multiple inheritance.

Notes

Every concrete AbstractPointSymmetricPolytope must define the following functions:

  • from AbstractPointSymmetric:

    • center(::AbstractPointSymmetricPolytope{N})::Vector{N} – return the center point

  • from AbstractPolytope:

    • vertices_list(::AbstractPointSymmetricPolytope{N})::Vector{Vector{N}} – return a list of all vertices

julia> subtypes(AbstractPointSymmetricPolytope)
5-element Array{Any,1}:
 AbstractHyperrectangle
 Ball1
 Interval
 LineSegment
 Zonotope
source

This interface defines the following functions:

LazySets.dim — Method.
dim(P::AbstractPointSymmetricPolytope)::Int

Return the ambient dimension of a point symmetric set.

Input

  • P – set

Output

The ambient dimension of the set.

source
LazySets.an_element — Method.
an_element(P::AbstractPointSymmetricPolytope{N})::Vector{N} where {N<:Real}

Return some element of a point symmetric polytope.

Input

  • P – point symmetric polytope

Output

The center of the point symmetric polytope.

source

Hyperrectangle

A hyperrectangle is a special point symmetric polytope with axis-aligned facets.

LazySets.AbstractHyperrectangle — Type.
AbstractHyperrectangle{N<:Real} <: AbstractPointSymmetricPolytope{N}

Abstract type for hyperrectangular sets.

Notes

Every concrete AbstractHyperrectangle must define the following functions:

  • radius_hyperrectangle(::AbstractHyperrectangle{N})::Vector{N} – return the hyperrectangle's radius, which is a full-dimensional vector

  • radius_hyperrectangle(::AbstractHyperrectangle{N}, i::Int)::N – return the hyperrectangle's radius in the i-th dimension

julia> subtypes(AbstractHyperrectangle)
4-element Array{Any,1}:
 AbstractSingleton
 BallInf
 Hyperrectangle
 SymmetricIntervalHull
source

This interface defines the following functions:

Base.LinAlg.norm — Method.
norm(S::LazySet, [p]::Real=Inf)

Return the norm of a convex set. It is the norm of the enclosing ball (of the given $p$-norm) of minimal volume that is centered in the origin.

Input

  • S – convex set

  • p – (optional, default: Inf) norm

Output

A real number representing the norm.

source
norm(H::AbstractHyperrectangle, [p]::Real=Inf)::Real

Return the norm of a hyperrectangular set.

Input

  • H – hyperrectangular set

  • p – (optional, default: Inf) norm

Output

A real number representing the norm.

Notes

The norm of a hyperrectangular set is defined as the norm of the enclosing ball, of the given $p$-norm, of minimal volume that is centered in the origin.

source
LazySets.radius — Method.
radius(S::LazySet, [p]::Real=Inf)

Return the radius of a convex set. It is the radius of the enclosing ball (of the given $p$-norm) of minimal volume with the same center.

Input

  • S – convex set

  • p – (optional, default: Inf) norm

Output

A real number representing the radius.

source
radius(H::AbstractHyperrectangle, [p]::Real=Inf)::Real

Return the radius of a hyperrectangular set.

Input

  • H – hyperrectangular set

  • p – (optional, default: Inf) norm

Output

A real number representing the radius.

Notes

The radius is defined as the radius of the enclosing ball of the given $p$-norm of minimal volume with the same center. It is the same for all corners of a hyperrectangular set.

source
LazySets.σ — Method.
σ(d::AbstractVector{N}, H::AbstractHyperrectangle{N}) where {N<:Real}

Return the support vector of a hyperrectangular set in a given direction.

Input

  • d – direction

  • H – hyperrectangular set

Output

The support vector in the given direction. If the direction has norm zero, the vertex with biggest values is returned.

source
Base.:∈ — Method.
∈(x::AbstractVector{N}, H::AbstractHyperrectangle{N})::Bool where {N<:Real}

Check whether a given point is contained in a hyperrectangular set.

Input

  • x – point/vector

  • H – hyperrectangular set

Output

true iff $x ∈ H$.

Algorithm

Let $H$ be an $n$-dimensional hyperrectangular set, $c_i$ and $r_i$ be the box's center and radius and $x_i$ be the vector $x$ in dimension $i$, respectively. Then $x ∈ H$ iff $|c_i - x_i| ≤ r_i$ for all $i=1,…,n$.

source
LazySets.vertices_list — Method.
vertices_list(H::AbstractHyperrectangle{N})::Vector{Vector{N}} where {N<:Real}

Return the list of vertices of a hyperrectangular set.

Input

  • H – hyperrectangular set

Output

A list of vertices.

Notes

For high dimensions, it is preferable to develop a vertex_iterator approach.

source

Singleton

A singleton is a special hyperrectangle consisting of only one point.

LazySets.AbstractSingleton — Type.
AbstractSingleton{N<:Real} <: AbstractHyperrectangle{N}

Abstract type for sets with a single value.

Notes

Every concrete AbstractSingleton must define the following functions:

  • element(::AbstractSingleton{N})::Vector{N} – return the single element

  • element(::AbstractSingleton{N}, i::Int)::N – return the single element's entry in the i-th dimension

julia> subtypes(AbstractSingleton)
2-element Array{Any,1}:
 Singleton
 ZeroSet
source

This interface defines the following functions:

LazySets.σ — Method.
σ(d::AbstractVector{N}, S::AbstractSingleton{N}) where {N<:Real}

Return the support vector of a set with a single value.

Input

  • d – direction

  • S – set with a single value

Output

The support vector, which is the set's vector itself, irrespective of the given direction.

source
Base.:∈ — Method.
∈(x::AbstractVector{N}, S::AbstractSingleton{N})::Bool where {N<:Real}

Check whether a given point is contained in a set with a single value.

Input

  • x – point/vector

  • S – set with a single value

Output

true iff $x ∈ S$.

Notes

This implementation performs an exact comparison, which may be insufficient with floating point computations.

source
LazySets.an_element — Method.
an_element(S::LazySet{N}) where {N<:Real}

Return some element of a convex set.

Input

  • S – convex set

Output

An element of a convex set.

source
an_element(P::AbstractPointSymmetricPolytope{N})::Vector{N} where {N<:Real}

Return some element of a point symmetric polytope.

Input

  • P – point symmetric polytope

Output

The center of the point symmetric polytope.

source
LazySets.center — Method.
center(S::AbstractSingleton{N})::Vector{N} where {N<:Real}

Return the center of a set with a single value.

Input

  • S – set with a single value

Output

The only element of the set.

source
LazySets.vertices_list — Method.
vertices_list(S::AbstractSingleton{N})::Vector{Vector{N}} where {N<:Real}

Return the list of vertices of a set with a single value.

Input

  • S – set with a single value

Output

A list containing only a single vertex.

source
LazySets.radius_hyperrectangle — Method.
radius_hyperrectangle(S::AbstractSingleton{N})::Vector{N} where {N<:Real}

Return the box radius of a set with a single value in every dimension.

Input

  • S – set with a single value

Output

The zero vector.

source
LazySets.radius_hyperrectangle — Method.
radius_hyperrectangle(S::AbstractSingleton{N}, i::Int)::N where {N<:Real}

Return the box radius of a set with a single value in a given dimension.

Input

  • S – set with a single value

Output

Zero.

source
LazySets.linear_map — Method.
linear_map(M::AbstractMatrix, S::AbstractSingleton{N}) where {N<:Real}

Concrete linear map of an abstract singleton.

Input

  • M – matrix

  • S – abstract singleton

Output

The abstract singleton of the same type of $S$ obtained by applying the linear map to the element in $S$.

source