Set Interfaces

Set Interfaces

This section of the manual describes the interfaces for different set types. Every set that fits the description of an interface should also implement it. This helps in several ways:

The interface functions are outlined in the interface documentation. See Common Set Representations for implementations of the interfaces.

Note

The naming convention is such that all interface names (with the exception of the main abstract type LazySet) should be preceded by Abstract.

The following diagram shows the interface hierarchy.

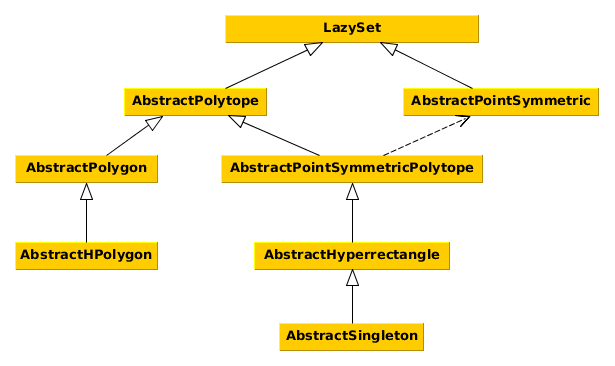
../assets/interfaces.png

LazySet

Every convex set in this library implements the main LazySet interface.

LazySets.LazySet — Type.
LazySet{N}

Abstract type for a lazy set.

Notes

Every concrete LazySet must define the following functions:

  • σ(d::AbstractVector{N}, S::LazySet)::AbstractVector{N} – the support vector of S in a given direction d

  • dim(S::LazySet)::Int – the ambient dimension of S

LazySet types should be parameterized with a type N, typically N<:Real, for using different numeric types.

source

Support function and support vector

Every LazySet type must define a function σ to compute the support vector.

LazySets.support_vector — Function.
support_vector

Alias for the support vector σ.

source
LazySets.ρ — Function.
ρ(d::AbstractVector{N}, S::LazySet{N})::N where {N<:Real}

Evaluate the support function of a set in a given direction.

Input

  • d – direction

  • S – convex set

Output

The support function of the set S for the direction d.

source
LazySets.support_function — Function.
support_function

Alias for the support function ρ.

source

Point symmetric set

Point symmetric sets such as balls of different norms are characterized by a center. Note that there is a special interface combination Point symmetric polytope.

LazySets.AbstractPointSymmetric — Type.
AbstractPointSymmetric{N<:Real} <: LazySet{N}

Abstract type for point symmetric sets.

Notes

Every concrete AbstractPointSymmetric must define the following functions:

  • center(::AbstractPointSymmetric{N})::Vector{N} – return the center point

julia> subtypes(AbstractPointSymmetric)
3-element Array{Union{DataType, UnionAll},1}:
 LazySets.Ball2
 LazySets.Ballp
 LazySets.Ellipsoid
source

Polytope

A polytope has finitely many vertices (V-representation) resp. facets (H-representation). Note that there is a special interface combination Point symmetric polytope.

LazySets.AbstractPolytope — Type.
AbstractPolytope{N<:Real} <: LazySet{N}

Abstract type for polytopic sets, i.e., sets with finitely many flat facets, or equivalently, sets defined as an intersection of a finite number of halfspaces, or equivalently, sets with finitely many vertices.

Notes

Every concrete AbstractPolytope must define the following functions:

  • vertices_list(::AbstractPolytope{N})::Vector{Vector{N}} – return a list of all vertices

julia> subtypes(AbstractPolytope)
3-element Array{Union{DataType, UnionAll},1}:
 LazySets.AbstractPointSymmetricPolytope
 LazySets.AbstractPolygon
 LazySets.HPolytope
source

Polygon

A polygon is a two-dimensional polytope.

LazySets.AbstractPolygon — Type.
AbstractPolygon{N<:Real} <: AbstractPolytope{N}

Abstract type for polygons (i.e., 2D polytopes).

Notes

Every concrete AbstractPolygon must define the following functions:

  • tovrep(::AbstractPolygon{N})::VPolygon{N} – transform into V-representation

  • tohrep(::AbstractPolygon{N})::AbstractHPolygon{N} – transform into H-representation

julia> subtypes(AbstractPolygon)
2-element Array{Union{DataType, UnionAll},1}:
 LazySets.AbstractHPolygon
 LazySets.VPolygon
source

HPolygon

An HPolygon is a polygon in H-representation (or constraint representation).

LazySets.AbstractHPolygon — Type.
AbstractHPolygon{N<:Real} <: AbstractPolygon{N}

Abstract type for polygons in H-representation (i.e., constraints).

Notes

Every concrete AbstractHPolygon must have the following fields:

  • constraints_list::Vector{LinearConstraint{N}} – the constraints

julia> subtypes(AbstractHPolygon)
2-element Array{Union{DataType, UnionAll},1}:
 LazySets.HPolygon   
 LazySets.HPolygonOpt
source

Point symmetric polytope

A point symmetric polytope is a combination of two other interfaces: Point symmetric set and Polytope.

LazySets.AbstractPointSymmetricPolytope — Type.
AbstractPointSymmetricPolytope{N<:Real} <: AbstractPolytope{N}

Abstract type for point symmetric, polytopic sets. It combines the AbstractPointSymmetric and AbstractPolytope interfaces. Such a type combination is necessary as long as Julia does not support multiple inheritance.

Notes

Every concrete AbstractPointSymmetricPolytope must define the following functions:

  • from AbstractPointSymmetric:

    • center(::AbstractPointSymmetricPolytope{N})::Vector{N} – return the center point

  • from AbstractPolytope:

    • vertices_list(::AbstractPointSymmetricPolytope{N})::Vector{Vector{N}} – return a list of all vertices

julia> subtypes(AbstractPointSymmetricPolytope)
3-element Array{Union{DataType, UnionAll},1}:
 LazySets.AbstractHyperrectangle
 LazySets.Ball1
 LazySets.Zonotope
source

Hyperrectangle

A hyperrectangle is a special point symmetric polytope with axis-aligned facets.

LazySets.AbstractHyperrectangle — Type.
AbstractHyperrectangle{N<:Real} <: AbstractPointSymmetricPolytope{N}

Abstract type for hyperrectangular sets.

Notes

Every concrete AbstractHyperrectangle must define the following functions:

  • radius_hyperrectangle(::AbstractHyperrectangle{N})::Vector{N} – return the hyperrectangle's radius, which is a full-dimensional vector

  • radius_hyperrectangle(::AbstractHyperrectangle{N}, i::Int)::N – return the hyperrectangle's radius in the i-th dimension

julia> subtypes(AbstractHyperrectangle)
4-element Array{Union{DataType, UnionAll},1}:
 LazySets.AbstractSingleton
 LazySets.BallInf
 LazySets.Hyperrectangle
 LazySets.SymmetricIntervalHull
source

Singleton

A singleton is a special hyperrectangle consisting of only one point.

LazySets.AbstractSingleton — Type.
AbstractSingleton{N<:Real} <: AbstractHyperrectangle{N}

Abstract type for sets with a single value.

Notes

Every concrete AbstractSingleton must define the following functions:

  • element(::AbstractSingleton{N})::Vector{N} – return the single element

  • element(::AbstractSingleton{N}, i::Int)::N – return the single element's entry in the i-th dimension

julia> subtypes(AbstractSingleton)
2-element Array{Union{DataType, UnionAll},1}:
 LazySets.Singleton
 LazySets.ZeroSet
source